[ 그래프 ]
그래프는 정점과 정점들을 연결하는 간선의 집합이다.
| 방향의 여부 | 방향 그래프, 무방향 그래프 |
| 순환 가능 여부 | 순환 그래프, 비순환 그래프 |
| 가중치가 있는 그래프 | 가중 그래프 |
[ 인접 배열 Array ]
정점 간의 관계를 2차원 배열로 나타낸 것이다.
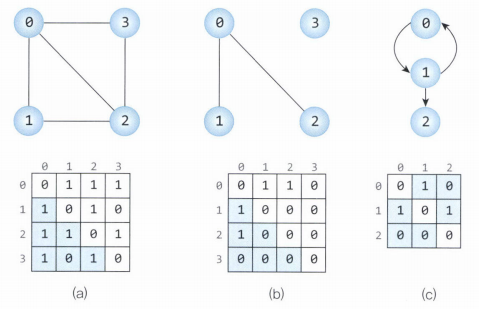
장점 : 간선 존재 여부를 상수시간 만에 알 수 있다.
단점 : 정점의 개수 V * V만큼의 메모리가 필요하다.
제한조건이 256MB인 경우 정수형 노드는 8192개 까지, 128MB인 경우 5792개 까지 가능하다.
[ 인접 리스트 vector, ArrayList ]
출발 정점을 기준으로 도착 정점들을 리스트 형태로 나열하는 방법이다.

장점 : 공간복잡도가 간선 개수에 의존한다.
단점 : 연결 상태를 확인하기 위해서 리스트를 하나씩 따라가 봐야 하기 때문에 O(N)의 시간 복잡도를 가진다.
제한조건이 인접 배열을 구성할 수 있는 크기라면 인접 배열로, 아니라면 인접 리스트로 문제를 푼다.
[ 예시 ]
> 제한 조건
시간 : 2초 이내
메모리 : 256MB
> 문제
1~N번까지의 노드와 M개의 단방향 간선이 존재한다. 각 간선의 거리는 1이다.
X번째 노드에서 출발해 최단 거리 k만큼 이동해 도착할 수 있는 모든 노드의 번호를 출력하라.
> 입력
노드 N (2 <= N <= 300,000)
도로 M (1 <= M <= 1,000,000)
거리 k (1 <= k <= 300,000)
출발지 X (1 <= X <= N)
> 계산
- 시간 복잡도
인접 배열과 인접 리스트 사용 둘 다 동일하다.
시간 복잡도 = O(N)
연산 시간 = N / 10^8 (또는 10^9)
최대 시간 복잡도 O(300,000) = 약 300,000 / 10^8 = 약 0.003 msec
- 인접 배열 VS 인접 리스트
그래프 생성을 위해서 N * N 크기의 메모리가 필요하다.
300,000 * 300,000 * 4 / (1024 * 1024) >= 256MB 이상
제한 조건 256MB를 초과하기 때문에 인접 배열의 사용이 불가하다.
이 문제는 인접 리스트를 이용해 풀이해야 한다.
- 인접 리스트 사용 시
M만큼의 메모리가 필요하다.
1,000,000 * 4 / (1024 * 1024) = 3.814 MB
'알고리즘' 카테고리의 다른 글
| 이분탐색 (Binary Search) (0) | 2025.02.04 |
|---|---|
| 기초(6) DFS, BFS (0) | 2025.01.24 |
| 기초(4) 난수 생성 (0) | 2025.01.24 |
| 기초(3) 리스트, 스택, 큐 (0) | 2025.01.24 |
| 기초(2) 시간와 공간복잡도 (0) | 2025.01.24 |
